Modulons !
Pour cette activité, nous allons mettre sur pause les apprentissages sur les concepts de la science informatique et nous concentrer sur des fonctionnalités de Scratch qui seront bien utiles dans un nombre de cas très variés : les extensions.
Ce sont des modules qui ajoutent des fonctionnalités à votre programmes en plus de celles déjà présentes. En plus des 9 familles de blocs classiques (Mouvement, Apparence, Son, Évènements,...), ce n'est pas moins de 11 familles supplémentaires qui sont actuellement disponibles.
4 sont utilisables sans matériel additionnel :
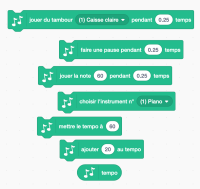
Musique
Stylo
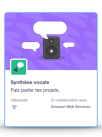
Synthèse vocale (avec internet)
Traduire (avec internet)
7 permettent d'avoir des fonctionnalités liées à matériel externe :
Détection vidéo (avec webcam)
Makey Makey
micro:bit
Lego Mindstorm EV3
Lego Boost
Lego Education WeDo 2.0
Go Direct Force & Acceleration
Cliquez sur les cadres pour trouver de plus amples explications
- 1 Synthèse vocale
Transforme un texte écrit en texte sonore. Nécessite un accès internet.
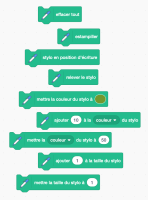
- 2 Stylo
Le stylo permet aux lutins de dessiner. Notamment les trajets qu'ils effectuent.
- 3 Musique
Permet de jouer de la musique de la même façon que pour des partitions.
- 4 Traduire
Permet d'obtenir la traduction d'un texte.Nécessite un accès internet.
- 5 Détection vidéo
Permet de détecter des mouvements devant la webcam, comme une Kinect basique.
- 6 Makey Makey
Permet de contrôler une carte Makey Makey. Elle se branche en USB sur l'ordinateur, puis se connecte à différents objets conducteurs de courants électriques pour créer des interfaces tangibles remplaçant le clavier ou la souris.
- 7 micro:bit
Permet de contrôler une mini ordinateur micro:bit. Il s'alimente en USB ou par piles et possède un capteur de mouvement 3D (ou accéléromètre) et un magnétomètre 3D (ou boussole numérique), des connectiques Bluetooth et USB, une matrice de 5 x 5 DEL (25 diodes électroluminescentes), un bouton de réinitialisation et deux boutons programmables. Il peut se connecter en Bluetooth LE, micro-USB ou les 5 anneaux d'entrée-sortie et 20 broches de connexion. Il est nécessaire d'installer le module Scratch Link (MacOS ou Windows).
- 8 Go Direct Force & Acceleration
Le capteur de force et d'accélération Vernier Go Direct est un outil scientifique qui permet de nouvelles façons de connecter le monde physique à vos projets Scratch. Mesurez la force lorsque vous poussez et tirez, et interagissez en secouant, tournant, faisant chuter et plus encore. Il est nécessaire d'installer le module Scratch Link (MacOS ou Windows).
- 9 Lego Mindstorms EV3
- 10 Lego Education WeDo 2.0
- 11 Lego Boost
Le module Stylo
À tout seigneur, tout honneur. Le module stylo est le Phénix des hôtes de la forêt des extensions Scratch. Depuis le Logo et sa tortue mécanique ou numérique, les professeurs de mathématiques ne rêvent qu'à cela quand il s'agit de faire de la programmation et de l'algorithmique : des carrés. Un peu comme le "Hello World !" de notre première activité. Alors que tous les tortues savent, qu'en fait, ce n'est qu'un cercle à 4 côtés. Démonstration…
Commençons d'abord par nous équiper de notre plus beau crayon de papier/crayon de bois/crayon à papier/crayon/crayon gris/crayon papier/crayon mine/crayon noir/crayon ordinaire (choisissez votre variante régionale préférée).
Il y a d'abord un lutin pour vous dans la bibliothèque Scratch :
Pensez à bien le replacer au centre de son espace Lutins :
Vous pouvez préférer une image provenant des emojis de votre ordinateur ou de votre tablette. Il suffit de l'ajouter à un champ texte. Ils sont en général plus stylisés que la bibliothèque interne de Scratch.
Vous devez également le placer correctement sur le repère de centrage, c'est moins facile parce que les bords sont plus larges que le dessin :
Maintenant, au travail :
Placez le crayon au milieu de la scène 
, mettez-le en position d'écriture 
et avancez de 40 pas 
.
Normalement, vous venez de dessiner votre premier polygone à 1 côté (en fait un segment). Remarquez qu'avant d'avancer, vous aviez dessiné un polygone à 0 côtés (un point finalement ?).
Revenez maintenant en (0,0).
La trace est toujours visible. En fait, vous avez ré-écrit par dessus en revenant au départ. Et du coup, vous avez dessiné votre premier véritable polygone (même si cela ne se voit pas) : un digone. Mais c'est un polygone dégénéré puisqu'il n'a pas d'aire (à ne pas confondre avec les polygones asphyxiés qui eux manquent d'air).
Vous avez maintenant besoin d'effacer votre feuille 
Et de relever votre stylo 
Ou inversement. Sinon, il continuera de dessiner quand des blocs lui donneront des ordres de déplacement. Et très vite, vous ne saurez plus ce que vous venez de dessiner.
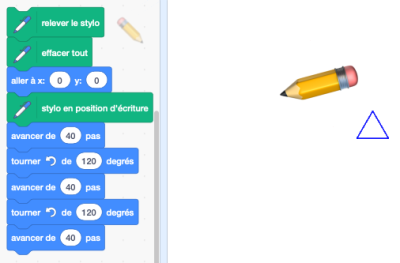
Passons au trigone régulier (ou plus communément appelé triangle équilatéral). Faites avancer de 40 pas, puis tournez vers la gauche (sens contraire aux aiguilles d'une montre ou sens trigonométrique) de 120 degrés 
Et encore, avancez de 40 pas, tournez à nouveau vers la gauche de 120° et avancez de 40 pas.
Vous devriez donc avoir avancé 3 fois de 40 pas en ayant tourné entre chaque étape de 120°, et donc être revenu au départ. Déplacez votre stylo avec la souris pour bien voir. Vous devriez avoir quelque chose comme la copie d'écran ci-contre.
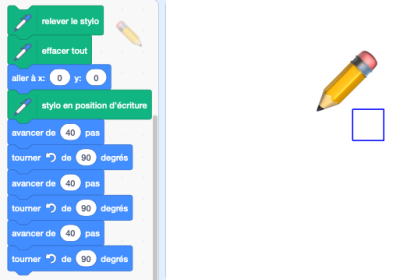
Changez maintenant les paramètres et ajoutez les blocs nécessaires pour dessiner un carré (ou savamment appelé tétragone).
Il vous a sans doute fallu remettre le crayon dans l'angle de départ, sinon le carré est en équilibre sur un de ses coins plutôt que d'être posé sur un côté. Deux possibilités :
rajouter un
à la fin,ou ajouter un
au début.
Au final vous devriez avoir ça :
Maintenant, paramétrons, bouclons et augmentons.
C'est à dire, remplaçons les valeurs qui sont les mêmes en plusieurs endroits par une variable. Il vous en faudra 2.
Ensuite remplaçons les instructions qui se répètent par une boucle contenant une seule occurrence de ces instructions.
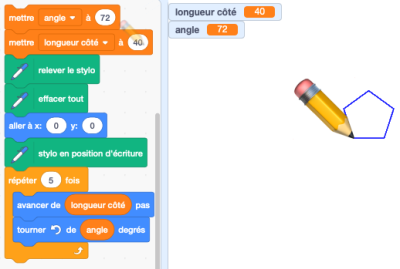
Enfin, remplaçons, l'initialisation des deux variables pour obtenir un pentagone. Un indice.
Vous devriez obtenir un script qui ressemble à cela :
Et puis, parce que vous n'êtes pas forcément enseignants de mathématiques, on a un petit secret à vous révéler : l'angle peut se calculer en fonction du nombre de côtés :
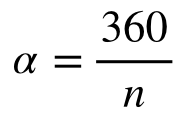
Ajoutez donc votre variable "nombre de côtés" et calculez l'angle en fonction de cette dernière. Cela vous permettra également de paramétrer la boucle répéter.
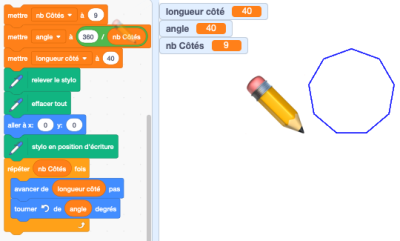
Profitez-en pour dessiner un Ennéagone.
La surface délimitées s'agrandit. Vous n'avez maintenant plus qu'un seul paramètre à modifier dans le programme pour changer la forme dessinée.
Profitez-en pour vérifier qu'il fonctionne toujours avec les petits nombres de côtés : 3, 4, ...
En fait, il fonctionne même avec 0 (un point), 1 (un segment) et 2 (deux segments superposés). Mais pas avec des nombres qui ne seraient pas entiers (essayez des nombres négatifs ou 3.7 par exemple, rassurez-vous, vous ne casserez rien).
On a quand même une limite à ce programme : essayez 20, puis 30. Avec 20 le dessin sort de la scène, et le crayon revient bien à son point de départ. Avec 30, non seulement il sort, mais il ne revient pas à son point de départ. En fait, quand un lutin s'éloigne de la scène, il se perd, essaie de toujours apparaitre sur la scène avec au moins un pixel en ne respectant pas totalement ses instructions de mouvement. Si vous le déplacer en y=1000, vous verrez y plafonner aux valeurs maximales de la scène (ymax = 180 modulo la taille du lutin).
20 côtés 
30 côtés 
Vous allez donc vous débrouiller pour garder le polygone sur la scène quel que soit le nombre de côtés. Pour cela, exprimons la longueur d'un côté en fonction de l'aire (qui sera une nouvelle variable de valeur fixée) et du nombre de côté.
On vous donne la formule ci-contre (les profs de math, ne regardez pas, cherchez la et envoyez-nous la démonstration qu'elle est correcte).
Il vous faut transformer cette formule en code Scratch. Vous trouverez 
et 
dans le menu déroulant de l'opérateur 
.
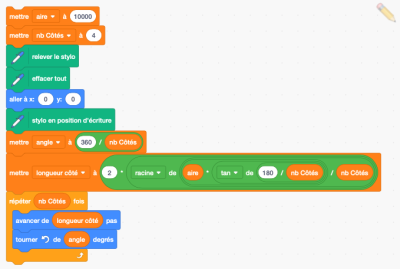
Scratch plaide coupable : c'est beaucoup moins lisible que la formule mathématique ci-dessus. Et beaucoup moins élégant, même si c'est affaire de goût. Par contre, c'est bien plus explicite quant à la priorité des opérations.
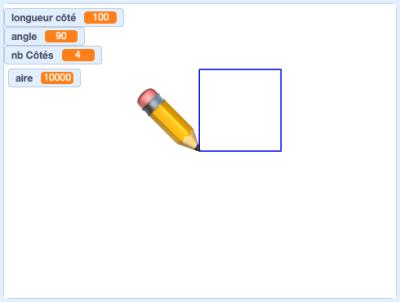
Faites tourner votre programme pour une aire de 10000 pixels carrés.
Obtenez-vous cela ?
Sinon, essayez de comparer votre script avec celui-là :
Dernière étape et non des moindres : généralisons et colorions
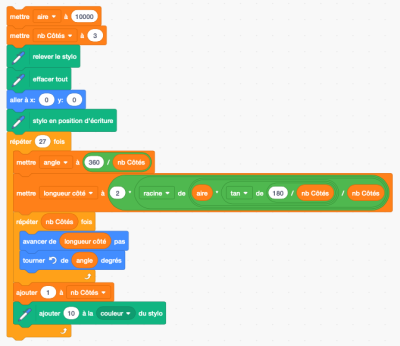
Vous allez faire maintenant en sorte de dessinez tous les polygones de 3 à 30 côtés et de faire varier la couleur de ces polygones.
On vous donne 3 blocs pour faire cela :
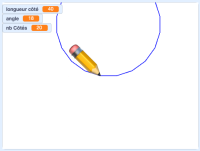
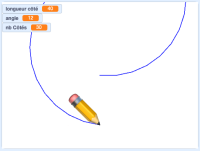
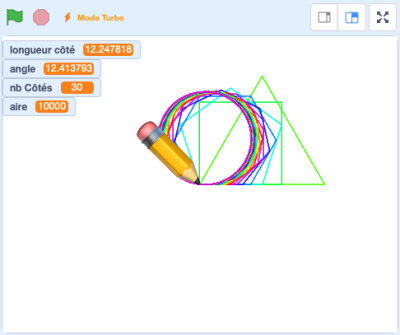
Vous devriez avoir un script qui ressemble plus ou moins à celui ci-contre et qui donne le graphique ci-dessous (aux couleurs près). On voit bien que plus on augmente le nombre de côtés, plus on se rapproche d'un cercle. Les tortues n'ont donc pas tout à fait tort (on vous épargnera la célèbre blague).
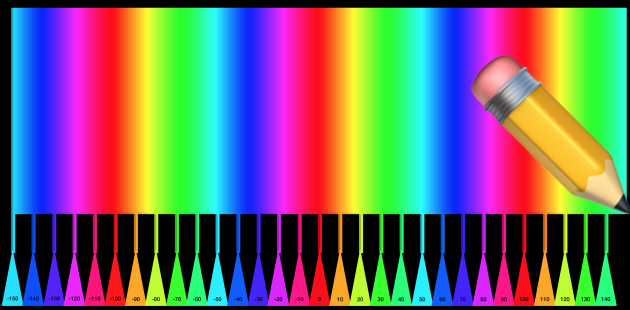
Profitons-en pour donner une explication sur la palette de couleurs.
Basé sur une roue chromatique, les valeurs de base vont de 0 (rouge) à 99 (presque rouge) en passant par toutes les couleurs de l'arc-en-ciel. Vous pouvez utiliser des nombres plus petits que 0 ou plus grands que 99, on recommence alors le cycle des couleurs (rien à voir avec les machines à laver). Ci-dessous un exemple de couleurs en fonction de la position x du lutin crayon.
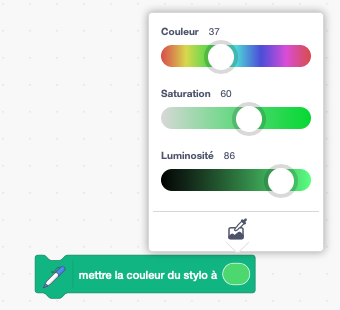
Il manque toutes les nuances incorporant le noir et le blanc, pour cela il faudra soit utiliser l'instruction "mettre la couleur du stylo à", sa décomposition des couleurs par code Couleur Saturation Luminosité ou bien sont outil pipette 
qui permet de sélectionner une couleur déjà existante à l'écran.
En dernier commentaire pour cette longue page, on vous recommande d'activer le mode turbo et de relancer votre programme. C'est comme cela que l'on peut utiliser le stylo pour dessiner de nombreuses lignes dans que l’œil humain ne voit tous ces processus. Dans de nombreux cas, la lenteur sera de mise (voire même programmée par des instructions "attendre..." pour que l'élève puisse se rendre compte à une vitesse humaine du déroulement du programme.
Passez ensuite aux fiches d'activité 7.